Algorithm Design
English | 中文
The quantization process represents a wide range of values as a small range of approximations, thus achieving lossy compression. For example: 16-bit JPG file into a 4-color GIF file, is to RGB color space color quantification into four colors of the process. In addition, four students who are 161,164,178,184 are represented as "one of the 160-169 stages, one in the 170-179 stage and one in the 180th stage" is also quantified. It is necessary to quantize the sequence of natural numbers less than 1000 into a sequence of s natural numbers. There are many ways to quantify, for example, only two numbers for the sequence {1 2 3 4 5 6 7 8 9 10}, can be expressed as {3 3 3 3 7 7 7 7 7}. Or can also be expressed in the form of {1 1 1 1 10 10 10 10 10}. What is the quantification result of the sum of the squares of the numerical errors?
For example, the sequence {1 2 3 4 5} is quantified to {2 2 3 3 3}, and the error after quantization is -1,0,0,1,2. Then the sum of the squared errors is 1 + 0 + 0 + 1 + 4 = 6. However, if the quantization becomes {2 2 4 4 4}, then the sum of the squares of errors is 1 + 0 + 1 + 0 + 1 = 3. Then write the program, use s values to quantify the sum of the sum of the squares after the given sequence.
The first row enters the number of test cases C (1 <= C <= 50). The length n (1 <= n <= 100) of the first line of the test cases and the number of available values s (1 <= s <= 10). The second line enters the n integer of the sequence, and all the numbers of the sequence are natural numbers below 1000.
Each test case will output the sum of the minimum squares generated when the given sequence is quantized with s values in one row.
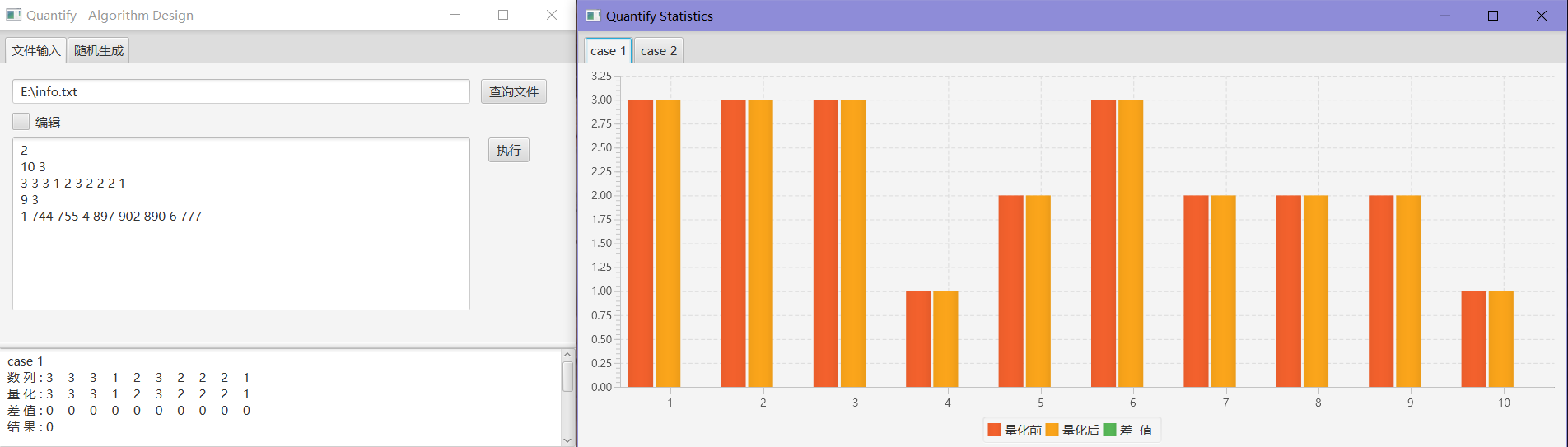
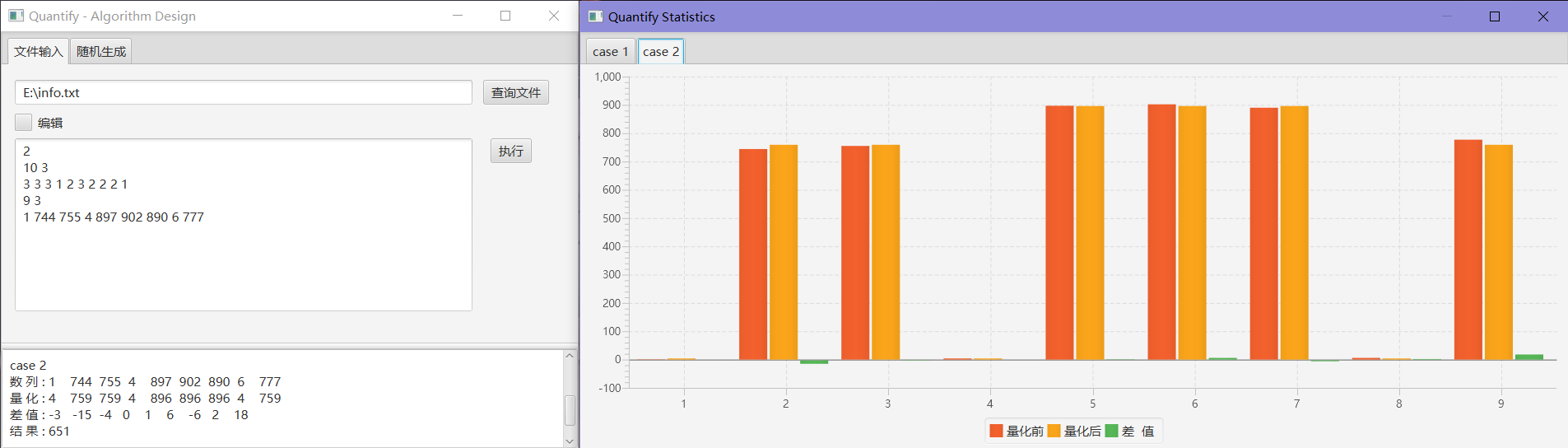
2
10 3
3 3 3 1 2 3 2 2 2 1
9 3
1 744 755 4 897 902 890 6 777
0
651